The recent announcement of Google [link] has gained a lot of attention [1]. Google Quantum AI announced their new quantum chip Willow, which demonstrates notable improvements in reliability and speed. In the next few paragraphs, we (Capgemini’s Quantum Lab) will try to put the announcement into perspective, both for the quantum field and for the industry that will undergo the impact from quantum computers in the coming years.
What does the announcement say?
It is important to understand that Google announced two results in their announcement of the Willow chip. First, they showed that they can correct errors in quantum hardware faster than they would occur. The second result, which was the result mainly picked up by the media, showed their quantum chip performed a calculation faster on a quantum computer than a classical computer could do. These results show that Willow is a world-leading superconducting chip with the best error correction demonstration.
Correcting errors
Building good quantum bits (qubits) is an immense engineering challenge, as the systems are susceptible to all sorts of environmental noise. This means that calculations fail when they are of a certain complexity. And because all useful quantum algorithms are beyond this complexity, quantum computers of today are extremely limited. Because of this limitation, researchers have theorised ways of combining multiple (noisy) physical qubits to create one logical qubit.
The goal is that this logical qubit is less noisy than the physical qubits and with their recent announcement, Google Quantum AI has shown that this goal is achievable. They have shown that using more physical qubits indeed lowers the error rate of the logical qubit and they have pushed this below the threshold. This means that their error-corrected (logical) qubit has a lower error rate than the individual qubits. Even more so, they showed that adding more qubits to a logical qubit indeed makes the logical qubit better.
Part of this demonstration is showing that the classical computing support system could meet the performance required for the implementation of quantum error correction, this is an extremely hard classical problem requiring massive data communication and processing. As part of this announcement, Google highlighted recent work they completed with Deepmind to improve performance through the application of machine learning.
Benchmarking performance
To benchmark the performance of their superconducting quantum chip, Google Quantum AI used random circuit sampling. This is a benchmark specifically well-suited for quantum computers and designed to be extremely hard for classical computers. The benchmark Willow performed would have taken today’s fastest supercomputer 1025 or 10 septillion years. For a layman that sounds truly impressive, and by all means, the quantum chip is impressive. But it is highly non-trivial to interpret the meaning of these results and numbers. It raises the question:
What do the results mean?
10 septillion years does not mean that much
The media are mostly talking about the “10 septillion years” number. However, other than to showcase quantum computing capabilities, random circuit sampling is of no use. In the original announcement, Google themselves even state that this is about the least commercially relevant activity you could do with a quantum computer. This is a typical example of comparing oranges with apples and should therefore not be taken too literally.
Error correction is on track
A more meaningful implication from Willow and its performance is the fact that the roadmap for error correction is realistic and that we are on track. When Peter Shor theorised quantum error correction in 1995 [2], the goal of error correction was to create logical qubits with errors (much) lower than possible with physical implementations of qubits. Willow has shown two different components of error correction.
- Adding more qubits decreases the logical error rate
When building upon physical (noisy) qubits to create logical qubits, the underlying qubits need to be at least of a certain baseline, and you need to be able to correct errors faster than they occur on average. When the physical qubits underlying the logical qubit are good enough, adding more physical qubits actually increases the performance of the logical qubit.
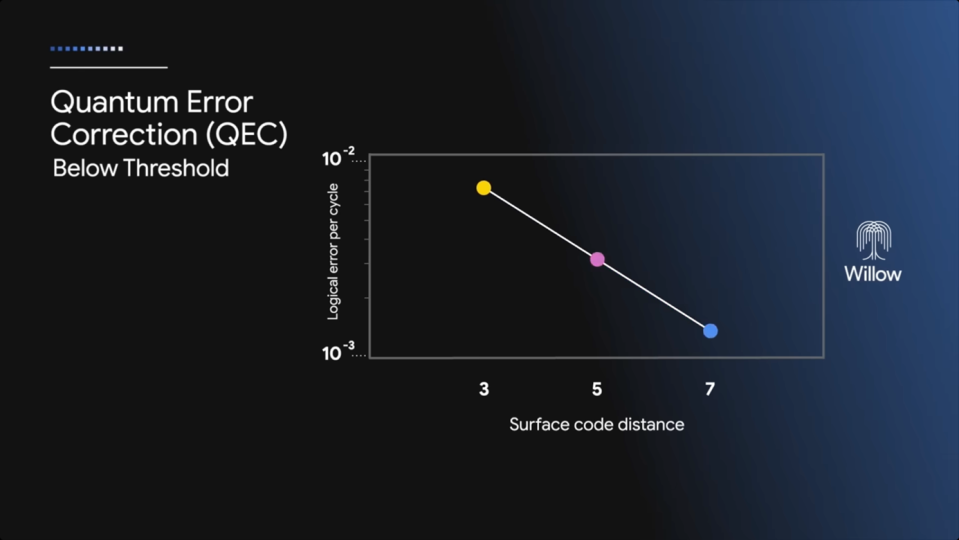
As can be seen in the figure, Willow’s physical qubits have shown to be good enough for this. I.e., when adding more qubits (a higher surface code), the logical error decreases. That is an important note, because when (physical) qubits are too noisy, adding more of them only increases the noise of the logical qubit.
2. Logical error rate is lower than physical error rate
In the advancements to large-scale quantum computers using error correction, logical qubits have been created before [3]. What is new with Willow is that the logical error is below the error of the individual physical (superconducting) qubits, thereby improving the performance, instead of worsening it. Moving beyond the error correction threshold with logical qubits is something that has not been done before on superconducting qubits, to the best of our knowledge.
What do the results change?
Most of the discussed results were already published in August 2024 and it created some buzz in the technical communities. Certainly, Google Quantum AI has shown high quality engineering and research, however, the press release and associated publicity made a lot more of it than was justified. It should be stated that the achievement from Willow it just another step along the path and does not mean we are at the large-scale fault tolerant quantum computers which can do anything useful, let alone break cryptographic standards. The main value of the work is to derisk quantum computing by showing that using more qubits leads to better logical qubits, i.e. with enough qubits we can achieve the error rates required. The use of quantum error correction is already a part of most roadmaps – not just Google Quantum AI.
The errors they achieved are still too high for useful calculations. Also, the expected timelines to commercial value or cryptographic threats are not impacted by Google Quantum AI’s result: this was an expected next step and not a step change. There is still a long way to go before quantum computers demonstrate commercial value and more effort is required into how this technology will be used when it comes.
What still needs to be done?
This result has further demonstrated that it is “when” not “if” for a future with quantum computers, but the quantum computing industry has a long way to go. We still need to understand practically how to use these future devices and where they will give us transformative value. Some potential applications and use cases are known in theory, but to realise them in practice, we need more than just better quantum hardware. Without clear and practical insights, quantum computers risks becoming impressively engineered paperweights with no commercial value. We need to start tackling the specifics and practicalities of quantum computing. There is a lot of investment and work in hardware (like Google Quantum AI’s Willow chip), but a lack of investment in algorithms and how we do something that is actually worthwhile.
Capgemini is working with clients and hardware companies to address these challenges, focusing on developing robust algorithms and practical applications. Our white paper, “Seizing the Commercial Value of Quantum Technology“, provides a comprehensive analysis of quantum technology’s current state and potential applications. By focusing on practical utility, we can ensure quantum computing delivers significant commercial value.
References
[1] R. Acharya et al., ‘Quantum error correction below the surface code threshold’, Aug. 24, 2024, arXiv: arXiv:2408.13687. Accessed: Aug. 27, 2024. [Online]. Available: http://arxiv.org/abs/2408.13687
[2] P. W. Shor, ‘Scheme for reducing decoherence in quantum computer memory’, Phys. Rev. A, vol. 52, no. 4, p. R2493, 1995.
[3] Y. Hong, E. Durso-Sabina, D. Hayes, and A. Lucas, ‘Entangling four logical qubits beyond break-even in a nonlocal code’, Phys. Rev. Lett., vol. 133, no. 18, p. 180601, 2024.

 English | EN
English | EN 